This Type of Signal is a Continuous Signal That Depends on Tim
- Slides: 9
Download presentation

Signal Types • Analog signals: continuous in time and amplitude – Example: voltage, current, temperature, … • Digital signals: discrete both in time and amplitude – Example: attendance of this class, digitizes analog signals, … • Discrete-time signal: discrete in time, continuous in amplitude – Example: hourly change of temperature in Austin • Theory for digital signals would be too complicated – Requires inclusion of nonlinearities into theory • Theory is based on discrete-time continuous-amplitude signals – Most convenient to develop theory – Good enough approximation to practice with some care • In practice we mostly process digital signals on processors – Need to take into account finite precision effects • Our text book is about theory hence its title – Discrete-Time Signal Processing ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ 1

Periodic (Uniform) Sampling • Sampling is a continuous to discrete-time conversion -3 -2 -1 0 1 2 3 4 • Most common sampling is periodic • • • T is the sampling period in second fs = 1/T is the sampling frequency in Hz Sampling frequency in radian-per-second s=2 fs rad/sec Use [. ] for discrete-time and (. ) for continuous time signals This is the ideal case not the practical but close enough – In practice it is implement with an analog-to-digital converters – We get digital signals that are quantized in amplitude and time ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ 2
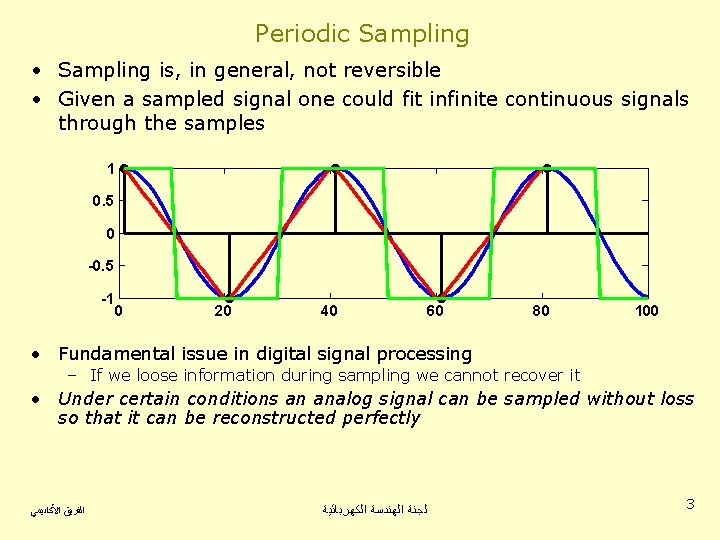
Periodic Sampling • Sampling is, in general, not reversible • Given a sampled signal one could fit infinite continuous signals through the samples 1 0. 5 0 -0. 5 -1 0 20 40 60 80 100 • Fundamental issue in digital signal processing – If we loose information during sampling we cannot recover it • Under certain conditions an analog signal can be sampled without loss so that it can be reconstructed perfectly ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ 3

Sampling Demo • In this movie the video camera is sampling at a fixed rate of 30 frames/second. • Observe how the rotating phasor aliases to different speeds as it spins faster. • Demo from DSP First: A Multimedia Approach by Mc. Clellan, Schafer, Yoder ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ 4
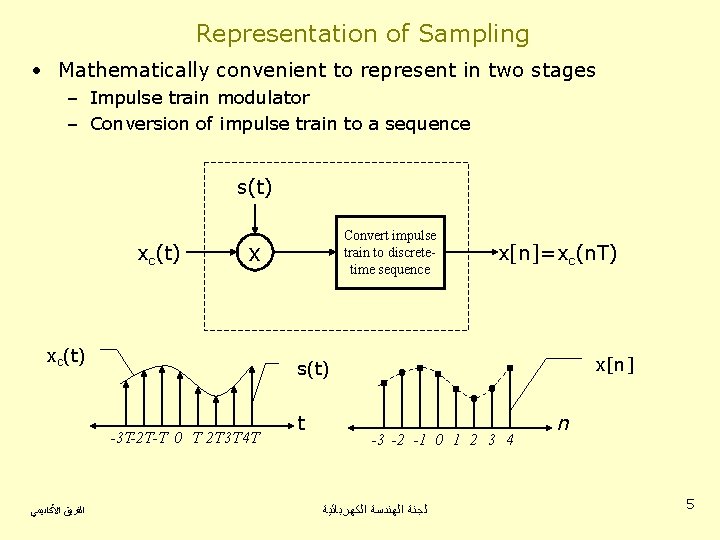
Representation of Sampling • Mathematically convenient to represent in two stages – Impulse train modulator – Conversion of impulse train to a sequence s(t) xc(t) x[n]=xc(n. T) x[n] s(t) -3 T-2 T-T 0 T 2 T 3 T 4 T ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ Convert impulse train to discretetime sequence t -3 -2 -1 0 1 2 3 4 ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ n 5

Continuous-Time Fourier Transform • Continuous-Time Fourier transform pair is defined as • We write xc(t) as a weighted sum of complex exponentials • Remember some Fourier Transform properties – Time Convolution (frequency domain multiplication) – Frequency Convolution (time domain multiplication) – Modulation (Frequency shift) ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ 6

Frequency Domain Representation of Sampling • Modulate (multiply) continuous-time signal with pulse train: • Let's take the Fourier Transform of xs(t) and s(t) • Fourier transform of pulse train is again a pulse train • Note that multiplication in time is convolution in frequency • We represent frequency with = 2 f hence s = 2 fs ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ 7

Frequency Domain Representation of Sampling • Convolution with pulse creates replicas at pulse location: • This tells us that the impulse train modulator – Creates images of the Fourier transform of the input signal – Images are periodic with sampling frequency – If s< N sampling maybe irreversible due to aliasing of images - N N s>2 N 3 s -2 s s - N N s 2 s 3 s s<2 N 3 s ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ -2 s s - N N s ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ 2 s 3 s 8
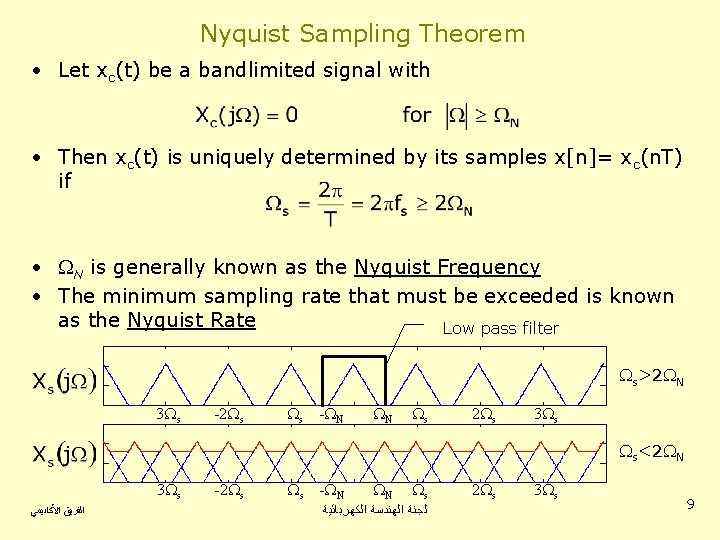
Nyquist Sampling Theorem • Let xc(t) be a bandlimited signal with • Then xc(t) is uniquely determined by its samples x[n]= xc(n. T) if • N is generally known as the Nyquist Frequency • The minimum sampling rate that must be exceeded is known as the Nyquist Rate Low pass filter s>2 N 3 s -2 s s - N N s 2 s 3 s s<2 N 3 s ﺍﻟﻔﺮﻳﻖ ﺍﻷﻜﺎﺩﻳﻤﻲ -2 s s - N N s ﻟﺠﻨﺔ ﺍﻟﻬﻨﺪﺳﺔ ﺍﻟﻜﻬﺮﺑﺎﺋﻴﺔ 2 s 3 s 9
Source: https://slidetodoc.com/signal-types-analog-signals-continuous-in-time-and/
0 Response to "This Type of Signal is a Continuous Signal That Depends on Tim"
Post a Comment